Gradient Boosting with XGBoost#
We illustrate the XGBoost model on a data set called “Hitters”, which includes 20 variables and 322 observations of major league baseball players.
The goal is to predict a baseball player’s salary on the basis of various features associated with performance in the previous year. We don’t cover the topic of exploratory data analysis in this notebook.
Visit this documentation if you want to learn more about the data
Setup#
You first need to install XGBoost:
conda install -c conda-forge py-xgboost
%matplotlib inline
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import warnings
warnings.simplefilter(action='ignore', category=FutureWarning)
import numpy as np
import matplotlib.pyplot as plt
import xgboost as xgb
print("XGB Version:", xgb.__version__)
from sklearn.metrics import mean_squared_error
from sklearn.inspection import permutation_importance
XGB Version: 1.7.1
Data#
# Import
df = pd.read_csv("https://raw.githubusercontent.com/kirenz/datasets/master/Hitters.csv")
# drop missing cases
df = df.dropna()
# Create dummies
dummies = pd.get_dummies(df[['League', 'Division','NewLeague']])
# Create our label y:
y = df[['Salary']]
X_numerical = df.drop(['Salary', 'League', 'Division', 'NewLeague'], axis=1).astype('float64')
# Make a list of all numerical features
list_numerical = X_numerical.columns
# Create all features
X = pd.concat([X_numerical, dummies[['League_N', 'Division_W', 'NewLeague_N']]], axis=1)
feature_names = X.columns
# Split data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=10)
# Data standardization
scaler = StandardScaler().fit(X_train[list_numerical])
X_train[list_numerical] = scaler.transform(X_train[list_numerical])
X_test[list_numerical] = scaler.transform(X_test[list_numerical])
# Make pandas dataframes
df_train = y_train.join(X_train)
df_test = y_test.join(X_test)
Model#
Define hyperparameters
params = {
"n_estimators":50,
"max_depth": 4,
"learning_rate": 0.01,
"eval_metric": "rmse",
"early_stopping_rounds": 5,
}
Prepare evaluation data
If there’s more than one item in eval_set, the last entry will be used for early stopping.
If we want to plot the learning curves for both training and test data, we need to provide both training and test data as eval_set
eval_set = [(X_train, y_train), (X_test, y_test)]
Build and fit model
reg = xgb.XGBRegressor(**params)
reg.fit(X_train,
y_train,
verbose=True,
eval_set= eval_set)
[0] validation_0-rmse:693.13939 validation_1-rmse:694.51649
[1] validation_0-rmse:687.25191 validation_1-rmse:688.37644
[2] validation_0-rmse:681.42445 validation_1-rmse:682.31515
[3] validation_0-rmse:675.64867 validation_1-rmse:677.35826
[4] validation_0-rmse:669.93320 validation_1-rmse:672.46290
[5] validation_0-rmse:664.27350 validation_1-rmse:666.60591
[6] validation_0-rmse:658.67121 validation_1-rmse:661.82838
[7] validation_0-rmse:653.12688 validation_1-rmse:656.90319
[8] validation_0-rmse:647.63961 validation_1-rmse:652.24138
[9] validation_0-rmse:642.19390 validation_1-rmse:646.64970
[10] validation_0-rmse:636.80992 validation_1-rmse:641.92285
[11] validation_0-rmse:631.48134 validation_1-rmse:637.27762
[12] validation_0-rmse:626.19614 validation_1-rmse:631.90670
[13] validation_0-rmse:620.97255 validation_1-rmse:627.37414
[14] validation_0-rmse:615.80413 validation_1-rmse:622.82286
[15] validation_0-rmse:610.68529 validation_1-rmse:618.45032
[16] validation_0-rmse:605.60407 validation_1-rmse:613.33537
[17] validation_0-rmse:600.57906 validation_1-rmse:609.34508
[18] validation_0-rmse:595.60970 validation_1-rmse:605.29294
[19] validation_0-rmse:590.69058 validation_1-rmse:601.35710
[20] validation_0-rmse:585.80052 validation_1-rmse:596.47644
[21] validation_0-rmse:580.97580 validation_1-rmse:592.68846
[22] validation_0-rmse:576.20465 validation_1-rmse:588.83853
[23] validation_0-rmse:571.47605 validation_1-rmse:585.00430
[24] validation_0-rmse:566.76789 validation_1-rmse:580.46276
[25] validation_0-rmse:562.13473 validation_1-rmse:576.72806
[26] validation_0-rmse:557.55151 validation_1-rmse:573.04329
[27] validation_0-rmse:552.98293 validation_1-rmse:568.56142
[28] validation_0-rmse:548.47424 validation_1-rmse:564.78179
[29] validation_0-rmse:544.02571 validation_1-rmse:561.24016
[30] validation_0-rmse:539.58015 validation_1-rmse:557.70367
[31] validation_0-rmse:535.22326 validation_1-rmse:554.25781
[32] validation_0-rmse:530.91185 validation_1-rmse:550.87278
[33] validation_0-rmse:526.59696 validation_1-rmse:546.80625
[34] validation_0-rmse:522.37363 validation_1-rmse:543.51320
[35] validation_0-rmse:518.14474 validation_1-rmse:539.55518
[36] validation_0-rmse:513.98339 validation_1-rmse:536.03011
[37] validation_0-rmse:509.83863 validation_1-rmse:532.21427
[38] validation_0-rmse:505.74956 validation_1-rmse:528.81269
[39] validation_0-rmse:501.70899 validation_1-rmse:525.42317
[40] validation_0-rmse:497.69725 validation_1-rmse:522.18693
[41] validation_0-rmse:493.72723 validation_1-rmse:519.00022
[42] validation_0-rmse:489.80529 validation_1-rmse:515.74005
[43] validation_0-rmse:485.91322 validation_1-rmse:512.64781
[44] validation_0-rmse:482.06295 validation_1-rmse:509.52443
[45] validation_0-rmse:478.25068 validation_1-rmse:506.52609
[46] validation_0-rmse:474.47971 validation_1-rmse:503.42672
[47] validation_0-rmse:470.70649 validation_1-rmse:500.40295
[48] validation_0-rmse:466.97397 validation_1-rmse:497.36221
[49] validation_0-rmse:463.27880 validation_1-rmse:494.61958
XGBRegressor(base_score=0.5, booster='gbtree', callbacks=None,
colsample_bylevel=1, colsample_bynode=1, colsample_bytree=1,
early_stopping_rounds=5, enable_categorical=False,
eval_metric='rmse', feature_types=None, gamma=0, gpu_id=-1,
grow_policy='depthwise', importance_type=None,
interaction_constraints='', learning_rate=0.01, max_bin=256,
max_cat_threshold=64, max_cat_to_onehot=4, max_delta_step=0,
max_depth=4, max_leaves=0, min_child_weight=1, missing=nan,
monotone_constraints='()', n_estimators=50, n_jobs=0,
num_parallel_tree=1, predictor='auto', random_state=0, ...)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
XGBRegressor(base_score=0.5, booster='gbtree', callbacks=None,
colsample_bylevel=1, colsample_bynode=1, colsample_bytree=1,
early_stopping_rounds=5, enable_categorical=False,
eval_metric='rmse', feature_types=None, gamma=0, gpu_id=-1,
grow_policy='depthwise', importance_type=None,
interaction_constraints='', learning_rate=0.01, max_bin=256,
max_cat_threshold=64, max_cat_to_onehot=4, max_delta_step=0,
max_depth=4, max_leaves=0, min_child_weight=1, missing=nan,
monotone_constraints='()', n_estimators=50, n_jobs=0,
num_parallel_tree=1, predictor='auto', random_state=0, ...)reg.evals_result()
{'validation_0': OrderedDict([('rmse',
[693.1393857817644,
687.251910336823,
681.4244486825938,
675.6486724934836,
669.9331957060579,
664.2735039780409,
658.671209041782,
653.1268798100191,
647.639606963932,
642.1938985362038,
636.8099213158795,
631.4813365059504,
626.1961417611866,
620.9725471757737,
615.8041338657043,
610.6852890748453,
605.6040657347364,
600.5790575659756,
595.6096960389444,
590.6905825682088,
585.8005198863074,
580.9758014008682,
576.2046450150377,
571.4760470741261,
566.767889207885,
562.1347310337889,
557.5515139366653,
552.9829316203304,
548.4742444704232,
544.0257116458743,
539.580154381951,
535.223258825213,
530.9118515684579,
526.5969631915748,
522.3736292449992,
518.1447439056208,
513.98339041067,
509.8386269079192,
505.74956087337966,
501.7089946678633,
497.6972510812428,
493.72722733765556,
489.80528828448985,
485.91321877813294,
482.0629503106967,
478.2506824740748,
474.47970550622546,
470.7064900045892,
466.9739728063445,
463.27879631757037])]),
'validation_1': OrderedDict([('rmse',
[694.5164913542402,
688.3764374445906,
682.3151532702786,
677.3582590211814,
672.4628989003214,
666.6059087893586,
661.828382190362,
656.9031869172235,
652.2413750710891,
646.6496957785371,
641.9228547034586,
637.2776215615506,
631.9067047861197,
627.3741448283788,
622.8228568933258,
618.4503207716183,
613.3353736633013,
609.3450808941212,
605.2929405305549,
601.3570998696786,
596.476439502,
592.6884623416338,
588.8385297352924,
585.0042993486803,
580.4627558767744,
576.7280633186635,
573.043293650581,
568.561421543709,
564.7817911843646,
561.2401620562998,
557.7036728408804,
554.2578132311166,
550.8727841910988,
546.8062486649543,
543.5132044476993,
539.555182177302,
536.0301120486204,
532.2142708827711,
528.8126933842323,
525.4231683723752,
522.1869348578584,
519.0002165116805,
515.7400461083421,
512.6478116927028,
509.52442998205976,
506.52609169547287,
503.4267241371655,
500.40295281777617,
497.3622109130281,
494.61957750664214])])}
The best iteration obtained by early stopping. This attribute is 0-based, for instance if the best iteration is the first round, then best_iteration is 0.
reg.best_iteration
49
The best score obtained by early stopping.
reg.best_score
494.61957750664214
Make predictions
y_pred = reg.predict(X_test)
Obtain RMSE
mean_squared_error(y_test, y_pred, squared = False)
494.61957203317934
Save the model (optional)
# Save model into JSON format.
# reg.save_model("regressor.json")
Plot training test deviance#
Obtain evaluation metrics
results = reg.evals_result()
Plot training test deviance
# Prepare x-axis
epochs = len(results['validation_0']['rmse'])
x_axis = range(0, epochs)
fig, ax = plt.subplots()
ax.plot(x_axis, results['validation_0']['rmse'], label='Train')
ax.plot(x_axis, results['validation_1']['rmse'], label='Test')
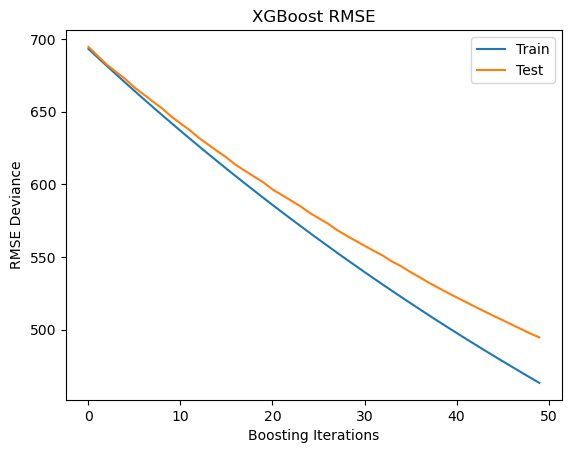
plt.title('XGBoost RMSE')
plt.xlabel("Boosting Iterations")
plt.ylabel("RMSE Deviance")
plt.legend(loc="upper right");
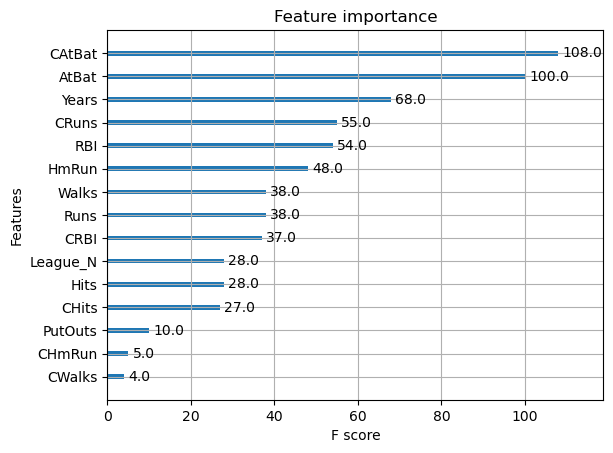
Feature importance#
Next, we take a look at the tree based feature importance and the permutation importance.
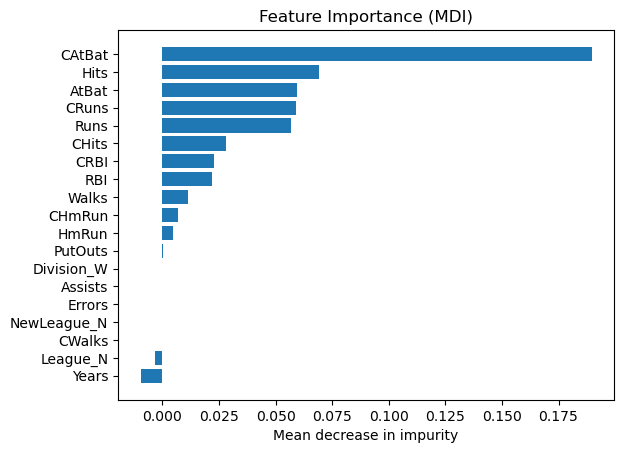
Mean decrease in impurity (MDI)#
Mean decrease in impurity (MDI) is a measure of feature importance for decision tree models.
Note
Visit this notebook to learn more about MDI
reg.feature_importances_
array([0.01666714, 0.04953949, 0.00669265, 0.08019661, 0.0286376 ,
0.1554871 , 0.02532776, 0.2681985 , 0.23080857, 0.0662018 ,
0.02479421, 0.03500974, 0.00164787, 0.0024867 , 0. ,
0. , 0.00830429, 0. , 0. ], dtype=float32)
reg.feature_names_in_
array(['AtBat', 'Hits', 'HmRun', 'Runs', 'RBI', 'Walks', 'Years',
'CAtBat', 'CHits', 'CHmRun', 'CRuns', 'CRBI', 'CWalks', 'PutOuts',
'Assists', 'Errors', 'League_N', 'Division_W', 'NewLeague_N'],
dtype='<U11')
Feature importances are provided by the function
plot_importance
xgb.plot_importance(reg);
Permutation feature importance#
The permutation feature importance is defined to be the decrease in a model score when a single feature value is randomly shuffled.
Note
Visit this notebook to learn more about permutation feature importance.
result = permutation_importance(
reg, X_test, y_test, n_repeats=10, random_state=42, n_jobs=2
)
feature_names
Index(['AtBat', 'Hits', 'HmRun', 'Runs', 'RBI', 'Walks', 'Years', 'CAtBat',
'CHits', 'CHmRun', 'CRuns', 'CRBI', 'CWalks', 'PutOuts', 'Assists',
'Errors', 'League_N', 'Division_W', 'NewLeague_N'],
dtype='object')
tree_importances = pd.Series(result.importances_mean, index=feature_names)
# sort features according to importance
sorted_idx = np.argsort(tree_importances)
pos = np.arange(sorted_idx.shape[0])
# plot feature importances
plt.barh(pos, tree_importances[sorted_idx], align="center")
plt.yticks(pos, np.array(feature_names)[sorted_idx])
plt.title("Feature Importance (MDI)")
plt.xlabel("Mean decrease in impurity");
Same data plotted as boxplot:
plt.boxplot(
result.importances[sorted_idx].T,
vert=False,
labels=np.array(feature_names)[sorted_idx],
)
plt.title("Permutation Importance (test set)")
plt.show()
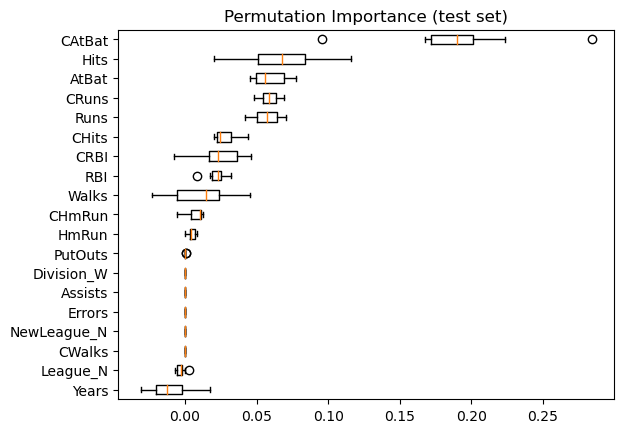
We observe that the same features are detected as most important using both methods. Although the relative importances vary (especially for feature
Years).

